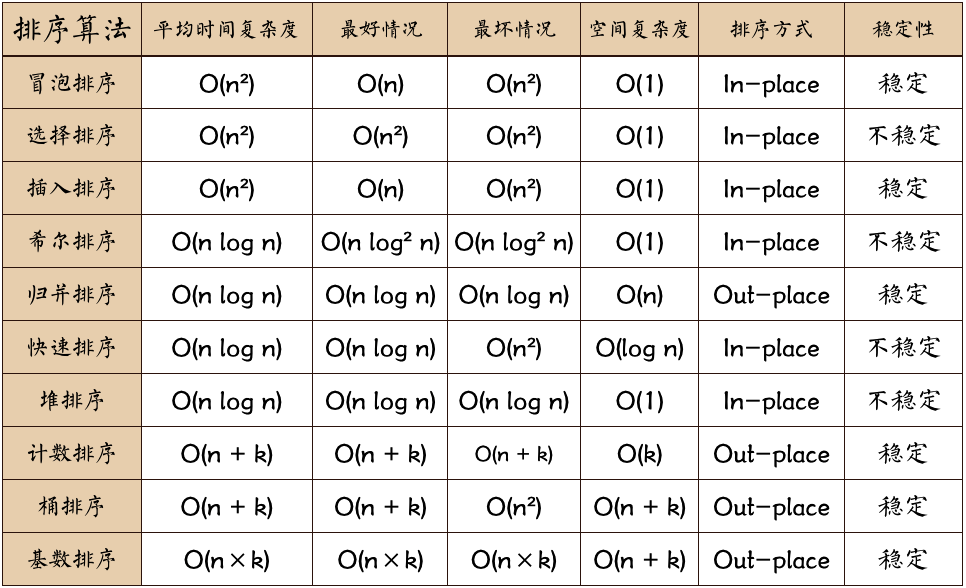
排序
输入:points = [[10,16],[2,8],[1,6],[7,12]]
输出:2
关键点
- 排序,找右边界
- 贪心
public int findMinArrowShots(int[][] points) {
if (points.length == 0) {
return 0;
}
Arrays.sort(points, new Comparator<int[]>() {
public int compare(int[] point1, int[] point2) {
if (point1[1] > point2[1]) {
return 1;
} else if (point1[1] < point2[1]) {
return -1;
} else {
return 0;
}
}
});
//[[1,6],[2,8],[7,12],[10,16]]
int pos = points[0][1];
int ans = 1;
for (int[] balloon: points) {
if (balloon[0] > pos) {//不断改变右边界
pos = balloon[1];
++ans;
}
}
return ans;
}
Q:以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
关键点
- 排序,找右边界
- 贪心
public int[][] merge(int[][] intervals) {
if (intervals.length == 0) {
return new int[0][2];
}
Arrays.sort(intervals, new Comparator<int[]>() {
public int compare(int[] interval1, int[] interval2) {
return interval1[0] - interval2[0];
}
});
List<int[]> merged = new ArrayList<int[]>();
for (int i = 0; i < intervals.length; ++i) {
int L = intervals[i][0], R = intervals[i][1];
if (merged.size() == 0 || merged.get(merged.size() - 1)[1] < L) {
merged.add(new int[]{L, R});
} else {
merged.get(merged.size() - 1)[1] = Math.max(merged.get(merged.size() - 1)[1], R);
}
}
return merged.toArray(new int[merged.size()][]);
}
public static int[] bubbleSort(int[] array) {
if (array.length == 0)
return array;
for (int i = 0; i < array.length; i++){
for (int j = 0; j < array.length - 1 - i; j++)//后i个元素已经排好序
if (array[j + 1] < array[j]) {
int temp = array[j + 1];
array[j + 1] = array[j];
array[j] = temp;
}
}
return array;
}

public static int[] selectionSort(int[] array) {
if (array.length == 0)
return array;
for (int i = 0; i < array.length; i++) {
int minIndex = i;
for (int j = i; j < array.length; j++) {
if (array[j] < array[minIndex]) //找到最小的数
minIndex = j; //将最小数的索引保存
}
int temp = array[minIndex];
array[minIndex] = array[i];
array[i] = temp;
}
return array;
}

public static int[] insertionSort(int[] array) {
if (array.length == 0)
return array;
int current;
for (int i = 0; i < array.length - 1; i++) {
current = array[i + 1];
int preIndex = i;
while (preIndex >= 0 && current < array[preIndex]) {
array[preIndex + 1] = array[preIndex];
preIndex--;
}
array[preIndex + 1] = current;
}
return array;
}
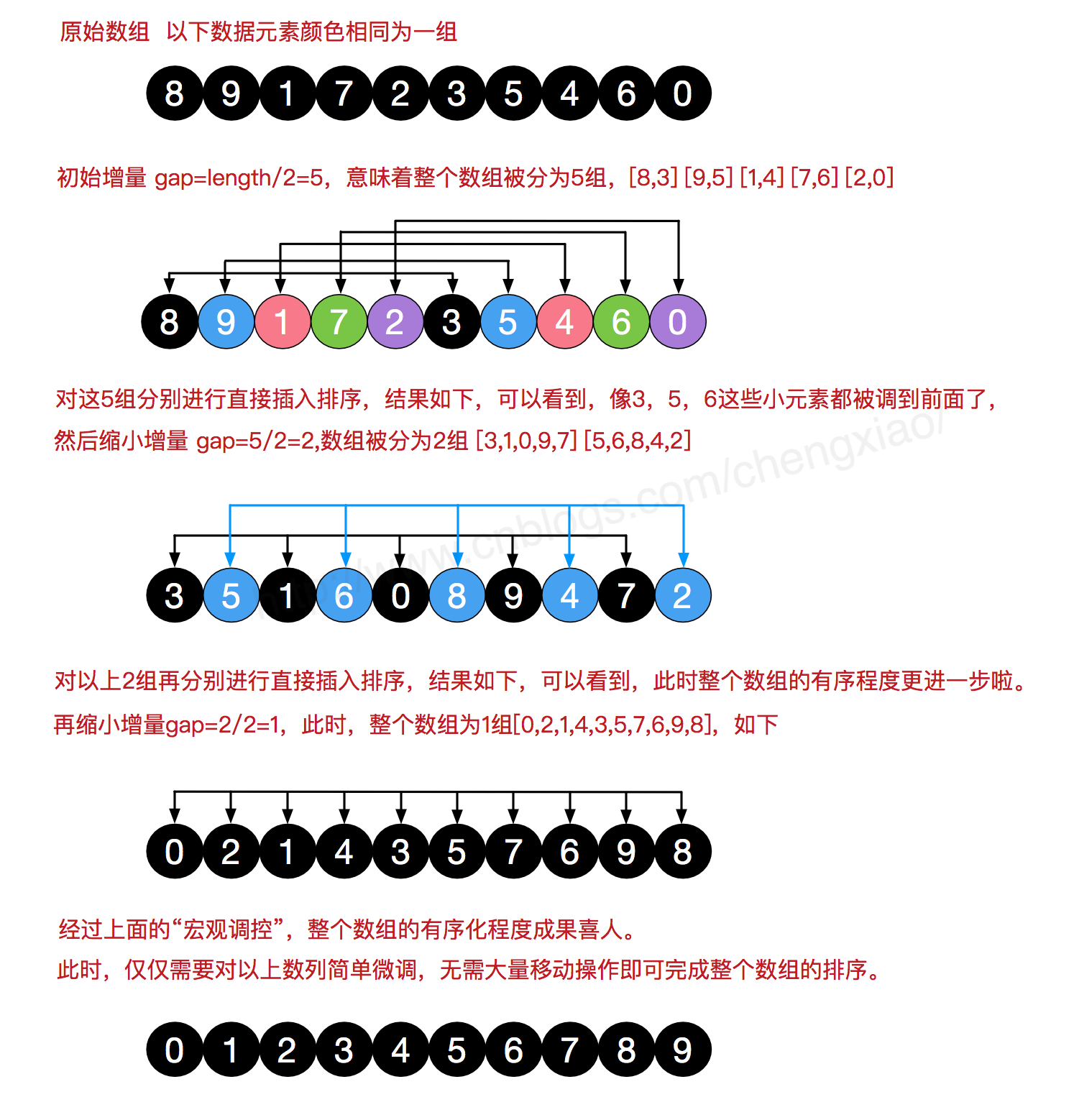
public static int[] ShellSort(int[] array) {
int len = array.length;
int temp, gap = len / 2;
while (gap > 0) {
for (int i = gap; i < len; i++) {
temp = array[i];
int preIndex = i - gap;
while (preIndex >= 0 && array[preIndex] > temp) {
array[preIndex + gap] = array[preIndex];
preIndex -= gap;
}
array[preIndex + gap] = temp;
}
gap /= 2;
}
return array;
}

public static int[] MergeSort(int[] array) {
if (array.length < 2) return array;
int mid = array.length / 2;
int[] left = Arrays.copyOfRange(array, 0, mid);
int[] right = Arrays.copyOfRange(array, mid, array.length);
return merge(MergeSort(left), MergeSort(right));
}
public static int[] merge(int[] left, int[] right) {
int[] result = new int[left.length + right.length];
for (int index = 0, i = 0, j = 0; index < result.length; index++) {
if (i >= left.length)
result[index] = right[j++];
else if (j >= right.length)
result[index] = left[i++];
else if (left[i] > right[j])
result[index] = right[j++];
else
result[index] = left[i++];
}
return result;
}

public static int[] QuickSort(int[] array, int start, int end) {
if (array.length < 1 || start < 0 || end >= array.length || start > end) return null;
int smallIndex = partition(array, start, end);
if (smallIndex > start)
QuickSort(array, start, smallIndex - 1);
if (smallIndex < end)
QuickSort(array, smallIndex + 1, end);
return array;
}
/**
* 快速排序算法——partition
* @param array
* @param start
* @param end
* @return
*/
public static int partition(int[] array, int start, int end) {
int pivot = (int) (start + Math.random() * (end - start + 1));
int smallIndex = start - 1;
swap(array, pivot, end);
for (int i = start; i <= end; i++)
if (array[i] <= array[end]) {
smallIndex++;
if (i > smallIndex)
swap(array, i, smallIndex);
}
return smallIndex;
}
/**
* 交换数组内两个元素
* @param array
* @param i
* @param j
*/
public static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
public static int[] HeapSort(int[] array) {
len = array.length;
if (len < 1) return array;
//1.构建一个最大堆
buildMaxHeap(array);
//2.循环将堆首位(最大值)与末位交换,然后在重新调整最大堆
while (len > 0) {
swap(array, 0, len - 1);
len--;
adjustHeap(array, 0);
}
return array;
}
/**
* 建立最大堆
*
* @param array
*/
public static void buildMaxHeap(int[] array) {
//从最后一个非叶子节点开始向上构造最大堆
for (int i = (len/2 - 1); i >= 0; i--) { //感谢 @让我发会呆 网友的提醒,此处应该为 i = (len/2 - 1)
adjustHeap(array, i);
}
}
/**
* 调整使之成为最大堆
*
* @param array
* @param i
*/
public static void adjustHeap(int[] array, int i) {
int maxIndex = i;
//如果有左子树,且左子树大于父节点,则将最大指针指向左子树
if (i * 2 < len && array[i * 2] > array[maxIndex])
maxIndex = i * 2;
//如果有右子树,且右子树大于父节点,则将最大指针指向右子树
if (i * 2 + 1 < len && array[i * 2 + 1] > array[maxIndex])
maxIndex = i * 2 + 1;
//如果父节点不是最大值,则将父节点与最大值交换,并且递归调整与父节点交换的位置。
if (maxIndex != i) {
swap(array, maxIndex, i);
adjustHeap(array, maxIndex);
}
}